The Triangle Law of Vector Addition articulates that when two vectors are illustrated in terms of their magnitude and direction by two consecutive sides of a triangle, the resultant vector’s magnitude and direction can be depicted by the remaining side of the triangle. Vectors, being quantities characterized by both magnitude and direction, offer a unique way of representing physical quantities.
Unlike scalar quantities, vectors do not adhere to the typical rules of algebra, necessitating the development of distinct equations to facilitate mathematical operations such as addition and subtraction on vectors. The Triangle Law of Vector Addition specifically addresses the addition of two vector quantities.
What is Vector Addition?
Vector addition involves the geometric combination of two or more vectors. Unlike scalar quantities, vectors possess both magnitude and direction, making their addition distinct. The direct summation of vectors without accounting for their respective directions leads to erroneous results. To accurately perform vector addition, the ‘Triangle Law of Vector Addition’ is employed.
This principle acknowledges the significance of vector direction and provides a systematic approach for calculating the resultant vector. By constructing a triangle where the vectors serve as sides, the third side of the triangle depicts the resultant vector’s magnitude and direction. This technique ensures that vector addition is executed correctly, considering both magnitude and orientation.
The rules governing vector addition encompass the following considerations:
1. The addition of scalar and vector quantities is not permissible.
2. The vectors being subjected to addition must share the same characteristics. For instance, the addition of velocity should exclusively involve velocity vectors and not be combined with other vector quantities.
Vector addition can be accomplished through the utilization of two fundamental principles, which are:
1. The Triangle Law of Vector Addition
2. The Parallelogram Law of Vector Addition
What is Triangle Law of Vector Addition?
The Triangle Law of Vector Addition serves as a fundamental concept within vector algebra, facilitating the process of vector addition. This law is employed when the terminal point of the first vector is connected to the initial point of the second vector, forming a triangle. Similarly, the initial point of the first vector is connected to the terminal point of the second vector, completing the triangle. This approach is also known as the “head-to-tail” method for vector addition, where vectors are effectively combined through the construction of a triangle connecting their terminal and initial points.
Triangle Law of Vector Addition:
“If two sides of a triangle are used to represent two vectors, considering their magnitudes and directions in sequence, then the third side of the triangle represents the magnitude and direction of the resultant vector, with the orders of magnitude and direction being reversed.”
To grasp the concept of this law visually, we can refer to the provided diagram:
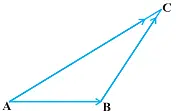
In this scenario, within the triangle ABC, we can effectively apply the principles of the triangle law of vector addition:
AC = AB + BC
Because AB and BC are arranged in the same sequence (where the starting point of one aligns with the ending point of the other), while AC is arranged in the reverse order, AC signifies the resultant value. This resultant vector is referred to as the vector composition.
Conditions for Triangle Law of Vector Addition
The Triangle Law of Vector Addition comes with specific conditions that apply to the addition of two vectors. These conditions are outlined as follows:
1. The vectors intended for addition must be oriented in the same sequence, implying that the starting point of one vector must align with the ending point of the other vector.
2. If all three sides of the constructed triangle adhere to the same order, the resultant vector will be null, indicating a zero result.
3. Vector addition adheres to the commutative property. In other words:
→ a + → b = → b + → a
4. Furthermore, vector addition conforms to the associative property of addition:
( → a + → b ) + → c = → a + ( → b + → c )
These conditions help establish the parameters within which the Triangle Law of Vector Addition operates, ensuring accurate and meaningful results when applying this principle.
Triangle Law of Vector Addition Derivation
The derivation of the Triangle Law of Vector Addition involves visualizing two vectors as sides of a triangle and understanding their relationship within that geometric context. Let’s derive this law step by step:
Consider two vectors →A and →B, which are to be added together.
Step 1: Draw Vector →A
Start by drawing vector →A with its initial point at the origin.
Step 2: Draw Vector →B
Draw vector →B with its initial point coinciding with the terminal point of vector →A.
Step 3: Complete the Triangle
Complete the triangle by drawing a line connecting the terminal point of →A to the initial point of →B. This line represents the resultant vector →R.
Step 4: Analyzing the Triangle
Now, we have a triangle with sides representing vectors →A, →B, and →R.
According to the Triangle Law of Vector Addition:
1. The sum of vectors →A and →B is represented by the vector →R.
2. The direction of vector →R is opposite to the direction of the side connecting →A and →B.
In other words, if we consider vector →A as the first side of the triangle and vector →B as the second side, then the resultant vector →R corresponds to the third side, but in the opposite direction.
Mathematically, this can be represented as:
→R = →B – →A
This derivation visually illustrates how the Triangle Law of Vector Addition works. By constructing a triangle using the vectors’ directions and magnitudes, we can intuitively determine the magnitude and direction of the resultant vector without performing complicated calculations.
Things to Remember
- Vectors are mathematical entities characterized by both magnitude and direction.
- There are two primary laws governing the addition of vectors: the Triangle Law of Vector Addition and the Parallelogram Law of Vector Addition.
- According to the Triangle Law of Vector Addition, when two vectors are depicted as two sides of a triangle, their resultant is accurately portrayed by the third side of the triangle.
- The resultant vector, arising from the addition of two vectors, is known as the vector composition.
- The magnitude of the resultant vector can be calculated using the formula:
R = √(P^2 + 2PQcosθ + Q^2) - Here, P and Q represent the magnitudes of the two vectors being added, and θ signifies the angle between them. This formula allows for the determination of the resultant vector’s magnitude without the need for complex computations, providing a valuable tool in vector analysis.
Sample Questions
→R = →A + →B
→R = (3i + 4j) + (2i – j)
→R = 5i + 3j
→R = →X + →Y
→R = (4i – 2j) + (-3i + j)
→R = i – j
→C = →A + →B
→C = (2i + 3j) + (-i + 4j)
→C = i + 7j
Car’s velocity →V_car = 20i m/s (eastward)
Wind’s velocity →V_wind = -5j m/s (southward)
Resultant velocity →V_resultant = →V_car + →V_wind
→V_resultant = 20i – 5j m/s
Given: P = 5 units, Q = 3 units, θ = 60 degrees
Using the formula: R = √(P^2 + 2PQcosθ + Q^2)
R = √(5^2 + 2 * 5 * 3 * cos(60°) + 3^2) R = √(25 + 30 + 9)
R = √64 R = 8 units
Conclusion
In conclusion, the Triangle Law of Vector Addition is a fundamental concept in vector algebra that allows us to combine vectors in a geometric manner. This law states that when two vectors are represented by the sides of a triangle, taken in order, the third side of the triangle represents the magnitude and direction of the resultant vector. This geometric approach is particularly useful when dealing with vectors that have both magnitude and direction.
By following the principles of the Triangle Law of Vector Addition, we can accurately determine the resultant vector of two given vectors. This law plays a pivotal role in various fields, including physics, engineering, and other mathematical applications where vectors are prevalent.






