In the realm of mathematics, certain concepts are fundamental to solving problems and understanding relationships between numbers. One such idea is the Least Common Multiple (LCM), a fundamental concept in many mathematical applications. In this article, we will explore the concept of LCM, consider its applicability, and outline some potential applications.
Table of Contents
- Introduction to LCM
- Definition and Calculation
- LCM vs. Greatest Common Divisor (GCD)
- Prime Factorization Method
- LCM of Fractions
- LCM in Real-World Scenarios
- LCM in Algebraic Expressions
- LCM and Divisibility
- Using LCM to Solve Word Problems
- LCM in Computer Science
- LCM and Music Rhythms
- Challenges in LCM Computation
- LCM in Competitive Programming
- LCM and Least Common Multiple Property
- Conclusion: Embracing the Versatility of LCM
Introduction to LCM
The Least Common Multiple (LCM) is a fundamental concept in mathematics that identifies the smallest multiple shared by two or more numbers. It plays a crucial role in various mathematical applications, from algebra to computer science. Calculating the LCM involves finding the smallest number divisible by each given number. This concept is vital for solving problems involving fractions, scheduling, and resource optimization. LCM’s versatility extends to music composition and competitive programming. Its understanding is essential for efficient problem-solving across diverse fields.
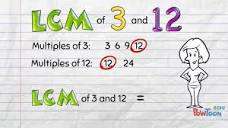
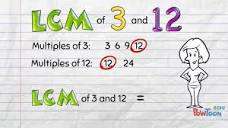
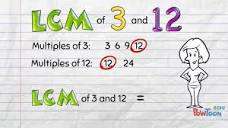
Definition and Calculation
LCM, or Least Common Multiple, is the smallest multiple that multiple numbers share. To calculate LCM, various methods like prime factorization and formulas can be used. It is distinct from the Greatest Common Divisor (GCD), which identifies the largest number dividing given numbers. LCM’s calculation involves finding the highest power of each prime factor in the numbers. This process ensures that the resulting LCM is the smallest multiple that all numbers can evenly divide into. LCM’s computation is integral in solving mathematical problems involving fractions, time intervals, and resource optimization, making it an essential concept in diverse fields.
LCM vs. Greatest Common Divisor
LCM (Least Common Multiple) and GCD (Greatest Common Divisor) are fundamental concepts in mathematics. LCM identifies the smallest shared multiple among numbers, while GCD determines the largest number by dividing those numbers without a remainder. LCM focuses on finding common multiples, vital in areas like scheduling and fractions. On the other hand, GCD is crucial for simplifying fractions and solving equations. These concepts have distinct roles but are equally important for various mathematical operations and problem-solving scenarios.
Prime Factorization Method
The prime factorization method is a technique used to calculate the Least Common Multiple (LCM) of numbers. It involves breaking down each number into its prime factors—irreducible prime numbers that multiply to form the original number. By identifying the highest power of each prime factor present in the given numbers, we can determine the LCM. This approach simplifies LCM calculation and is particularly useful for handling large numbers efficiently, making it an essential tool in various mathematical applications.
LCM of Fractions
The concept of LCM extends to fractions as well. When dealing with fractions, finding the LCM of their denominators is crucial. The LCM of the denominators ensures a common base for arithmetic operations involving fractions, such as addition, subtraction, and comparison. By determining the LCM of the denominators, fractions can be transformed into equivalent fractions with the same denominator, simplifying calculations and allowing for accurate comparisons and computations. This practice is essential for working with fractions in various mathematical and real-world scenarios.
LCM in Real-World Scenarios
LCM in Algebraic Expressions
LCM holds significance in algebraic expressions as well. When dealing with algebraic fractions or equations involving fractions, having a common denominator is essential for simplification and solving. LCM ensures that all expressions share the same denominator, facilitating operations like addition and subtraction of fractions. By using LCM to find a common base for algebraic expressions, the equations become more manageable and conducive to solving, allowing for accurate and streamlined algebraic manipulation in various mathematical contexts.
LCM and Divisibility
LCM has a direct connection to the concept of divisibility in mathematics. The LCM of two or more numbers is always a multiple of their common factors. This relationship is crucial for divisibility tests, as it helps determine whether a given number is divisible by another. By using the LCM to identify the common factors between numbers, we can efficiently assess their divisibility without the need for lengthy division calculations. This property of LCM aids in simplifying the process of identifying divisors and factors in various mathematical situations.
Using LCM to Solve Word Problems
Using the LCM to solve word problems is a powerful strategy in mathematics. When faced with scenarios involving multiple entities with distinct time or quantity intervals, the LCM helps pinpoint the least common instance when these events coincide. This is especially useful for synchronization, scheduling, and resource allocation. By finding the LCM of the intervals or quantities involved, we can determine when various events align, enabling effective planning and decision-making in real-world situations that demand coordination and optimization.
LCM in Computer Science
In computer science, LCM holds practical significance. It plays a role in scheduling tasks, memory allocation, and process synchronization. By determining the LCM of time intervals or periods, computer systems can efficiently manage resources and coordinate actions. This ensures tasks are executed optimally and concurrently, preventing resource clashes or wastage. LCM’s application in computer science contributes to improved performance and resource utilization, making it a valuable tool in designing efficient algorithms and systems for a wide range of applications.
LCM and Music Rhythms
Even in the realm of music, LCM finds relevance. Musicians utilize the concept of LCM to create harmonious rhythms and synchronized beats. By identifying the least common multiple of different time signatures or rhythm patterns, musicians can craft compositions with seamless transitions and coordinated musical elements. This ensures a pleasing auditory experience by aligning musical phrases and accents, demonstrating how mathematical concepts like LCM have artistic applications that contribute to the creation of captivating musical arrangements.
Challenges in LCM Computation
Computation of LCM, while valuable, comes with challenges. Particularly with large numbers, the process can be complex and time-consuming. The prime factorization method, although efficient, can become cumbersome as numbers grow. Additionally, identifying common prime factors becomes intricate when dealing with multiple numbers. These challenges necessitate the use of advanced algorithms and techniques to streamline LCM calculation. Balancing computational efficiency with accuracy poses a continuous challenge, especially in fields like cryptography, where LCM computation is pivotal for secure systems and protocols.
LCM in Competitive Programming
In competitive programming, LCM is a potent technique. It’s used to optimize algorithms, especially in scenarios involving time intervals or periodic events. By employing LCM, programmers can streamline resource usage, reduce computation, and solve problems with greater efficiency. This strategic application helps achieve better time complexity, enhancing performance in coding competitions. The versatility of LCM aids in devising quick solutions, giving programmers a competitive advantage in time-sensitive scenarios, and showcasing its significance in the realm of competitive programming.
LCM and Least Common Multiple Property
LCM holds a unique property that proves valuable in mathematical proofs and problem-solving. This property asserts that the LCM of two numbers is an upper bound for their product. In other words, the product of two numbers cannot exceed their LCM. This property is utilized to establish bounds, inequalities, and relationships in various mathematical contexts. By understanding and applying this property, mathematicians can derive insights and solutions in diverse mathematical disciplines, showcasing the intrinsic significance of LCM’s property in mathematical exploration.
Conclusion: Embracing the Versatility of LCM
The Least Common Multiple (LCM) is a flexible mathematical notion that has applications across a wide range of fields. LCM exhibits its aptitude for problem-solving and resource optimization by its involvement in algebraic equations, as well as through its relevance in computer science and real-world circumstances. Let’s not ignore the strength and relevance that LCM brings to the table as we continue to delve into the depths of mathematics.
VC- Frequently Asked Questions(FAQs)
While LCM focuses on finding the least common multiple, GCD identifies the largest number dividing two or more numbers.
To find the LCM of fractions, determine the LCM of their denominators to ensure a common denominator for arithmetic operations.
Yes, musicians use LCM to create rhythmic patterns and harmonious beats in their compositions.
Computing the LCM of large numbers can be computationally complex, often requiring advanced algorithms.
In competitive programming, LCM helps optimize resource usage and solve problems efficiently, contributing to better performance.






