Want create site? Find Free WordPress Themes and plugins.
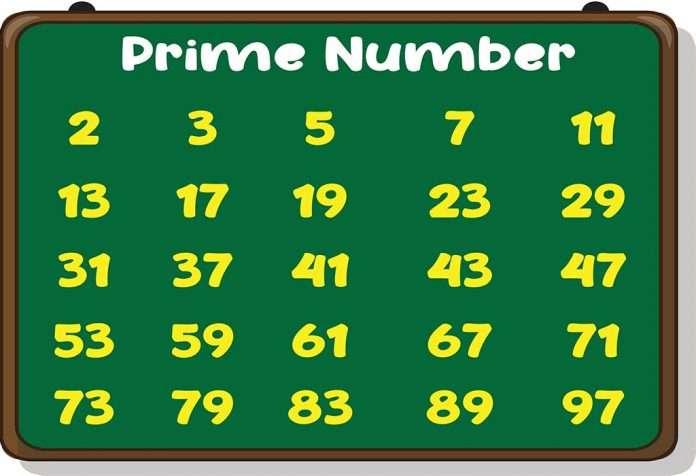
Understanding Prime Numbers
Characteristics of Prime Numbers
- Divisibility: Prime numbers have exactly two distinct positive divisors: 1 and themselves.
- Smallest Prime: The smallest prime number is 2, which is also unique as the only even prime number.
- Odd Primes: All prime numbers greater than 2 are odd, as any even number greater than 2 can be divided by 2.
- Infinite Nature: There are infinitely many prime numbers, a fact established by Euclid over two millennia ago.
- Distribution: Prime numbers become less frequent as numbers get larger, but they never completely disappear.
- Prime Factorization: Every integer greater than 1 can be uniquely represented as a product of prime numbers, according to the Fundamental Theorem of Arithmetic.
- No Patterns: Prime numbers do not follow a regular pattern or sequence, making their distribution seemingly random.
- Prime Gaps: The gaps between consecutive prime numbers vary and can be large, but there is always another prime eventually.
- Twin Primes: Some primes come in pairs called twin primes, which differ by exactly 2 (e.g., 11 and 13, 17 and 19).
- Special Forms: Some primes have special forms, such as Mersenne primes (2^p – 1) and Fermat primes (2^(2^n) + 1).
- Applications in Cryptography: Prime numbers are fundamental in modern cryptographic algorithms, ensuring secure communication.
- Primality Testing: Several methods, such as the Sieve of Eratosthenes and advanced computational algorithms, are used to test the primality of numbers.
- Prime Number Theorem: This theorem describes the asymptotic distribution of prime numbers among the positive integers, providing an approximation of their density.
- Biological Occurrence: Primes appear in nature, such as the periodic life cycles of cicadas that use prime numbers to avoid predators.
- Unpredictability: Despite extensive research, predicting the occurrence of the next prime number remains a challenge.
Finding Prime Numbers
Conclusion
FAQs
Q: 1 How many prime numbers are there between 1 and 100?
Ans:: There are 25 prime numbers between 1 and 100.
Q: 2 What is the smallest prime number between 1 and 100?
Ans: The smallest prime number between 1 and 100 is 2.
Q:3What is the largest prime number between 1 and 100?
Ans: The largest prime number between 1 and 100 is 97.
Q: 4Are all odd numbers between 1 and 100 prime?
Ans: No, not all odd numbers between 1 and 100 are prime. Only specific odd numbers that have no divisors other than 1 and themselves are prime.
Did you find apk for android? You can find new Free Android Games and apps.
